Equazioni: c’è chi rifugge la matematica come la peste, altri invece la vorrebbero sposare seduta stante. Nessuno può però negare che le equazioni siano state davvero rivoluzionarie. Ian Stewart, nel suo libro “17 equazioni che hanno cambiato il mondo“, ha spiegato l’impatto che la matematica ha avuto non solo in ambito scientifico, ma anche sulla filosofia: le equazioni matematiche giocano un ruolo fondamentale nella creazione del mondo come oggi lo conosciamo.
Ecco qui le 10 equazioni che hanno rivoluzionato il nostro modo di vivere. Non assisterete ad una lezione di fisica quantistica, state tranquilli! Solo ad un divertente elenco di numeri che non pensavate mai di considerare al di fuori dei vostri eserciziari di analisi. Oppure di non considerare affatto! Si tengano lontano i deboli di cuore, giusto per sicurezza!
Ispirandoci al video di Klesha Production, vi proponiamo un breve ma “cervellotico” viaggio nel mondo della matematica!
IL TEOREMA DI PITAGORA

“Il quadrato costruito sull’ipotenusa è uguale alla somma dei quadrati costruiti sui cateti”. L’equazione risale addirittura al 530 a.C. e c’è gente che, dopo tutto questo tempo, non la conosce ancora!
LA LEGGE DI GRAVITAZIONE UNIVERSALE

“La forza che attrae due corpi è direttamente proporzionale al prodotto delle due masse e inversamente proporzionale alle distanza”.
In soldoni: la forza di attrazione aumenta se la distanza fra due corpi diminuisce e aumenta se i corpi sono pesanti. Questo non basta a spiegare perché i ciccioni si innamorano prima, però!
LA FORMULA DI EULERO PER I POLIEDRI

L’equazione mette in relazione il numero delle facce (F), degli spigoli (S) e dei vertici (V) di un poliedro, ovvero i “solidi appuntiti” come l’icosaedro che trotterella allegramente qui sopra!
L’EQUAZIONE D’ONDA

L’equazione (qui presente in due varianti) è nota anche come equazione di d’Alembert. Essa indica la propagazione delle onde secondo variabili di tipo spaziale (x) e temporali (t). In sostanza: un’onda si muove nello spazio e nel tempo. Addentrarsi qui sarebbe rischioso! Molto rischioso!
LA TRASFORMATA DI FOURIER

Impossibile? Certo! Ma non per le menti brillanti! La trasformata di Fourier è una formula molto utile se volete studiare delle onde complesse. In parole povere, un’onda può presentarsi come un rumore e quindi essere più o meno complessa. Grazie alla formula di Fourier, è possibile “scomporre” l’onda complessa (in rosso nell’immagine) in tante altre piccole onde di andamento più semplice. Insomma: trattiamo un’onda complessa come una somma di onde più semplici!
EQUAZIONE DI NAVIER-STOKES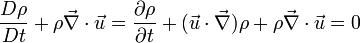
Una delle tante equazioni di Navier-Stokes che descrivono il comportamento di un fluido a livello macroscopico. Quando bevete il tè con gli amici, pensate a Navier-Stokes, ignoranti!
LA SECONDA LEGGE DELLA TERMODINAMICA

Torniamo a qualcosa di più leggibile. L’equazione della seconda legge della termodinamica vede come suo padre Boltzmann, anche se la sua formulazione è leggermente diversa. Uno degli enunciati della seconda legge della termodinamica recita che in un sistema fisico il disordine, o entropia, tende sempre a crescere. Quindi non insultate vostra madre che vi chiede di rimettere in ordine la vostra camera. Piuttosto rispondetele con tono pacato: “E’ una questione di fisica!”. (L’immagine mostra uno dei modi di rappresentare il secondo principio attraverso la macchina di Carnot).
LA RELATIVITA’
E = mc2
La teoria della relatività è stata una vera e propria rivoluzione nel campo della scienza del ‘900. La famosa formula descrive l’energia di un corpo in funzione della sua massa. Ancora una volta chi ha qualche chilo di più vince su tutto, anche in fisica! Alla faccia dei modelli che non capiscono la relatività!
ENTROPIA DELL’INFORMAZIONE
![\mathbb{H}[X]= -\sum_{i=1}^N{\mathbb{P}(x_i) \cdot \log_b{\mathbb{P}(x_i)}}](https://upload.wikimedia.org/math/5/4/5/545bc5c4f3d635a9a8c90f03a71bab72.png)
La teoria di Shannon vuole descrivere l’informazione media contenuta in un messaggio emesso nell’ambito della teoria dell’informazione. Secondo tale teoria, l’informazione contenuta in un messaggio è tanto più grande quanto meno è probabile. Il concetto è spiegato in soldoni dal modello termodinamico presente in figura: è maggiore la probabilità che poche “palline” si dispongono nelle due zone del contenitore che avere tutte le “palline” (ovvero i dati informativi) da una sola parte. Ovvero: a maggior probabilità di contenuto informativo corrisponde una minor probabilità che questo possa avvenire. In poche parole: non si può sapere tutto. O meglio: è molto difficile sapere tutto! Avete capito? Beh altro non si può dire: si finirebbe per parlare aramaico…
EQUAZIONE DI BLACK-SCHOLES

Chiedete ad un economista: lui saprà certamente dirvi di cosa stiamo parlando… Si proprio ad un economista: l’equazione di Black-Scholes esprime proprio come calcolare il prezzo di un prodotto senza considerare le variabili di mercato come la mediazione di mercati stessi prima che una bistecca ti sia servita in tavola! Come per il tè con gli amici, siete ignoranti se andate a fare la spesa e, davanti a un pacchetto di brioches, non pensate a Black-Scholes!
Vi sorprende che la matematica sia arrivata fino a qua? Non avete visto ancora nulla!







